Simple Harmonic Motion:

Important features of SHM are summarized as:

• i. A body executing SHM always vibrates about a fixed position
• ii. Its acceleration is always directed towards the mean position.
• iii. The magnitude of acceleration is always directly proportional to its displacement from the mean position i.e., acceleration will be zero at the mean position while it will be maximum at the extreme positions.
• iv. Its velocity is maximum at the mean position and zero at the extreme positions.

Now we discuss different terms which characterize simple harmonic motion.

Vibration:

One complete round trip of a vibrating body about its mean position is called one vibration.

Time Period (T ):

The time taken by a vibrating body to complete one vibration is called time period.

Frequency ( f ):

The number of vibrations or cycles of a vibrating body in one second is called its frequency. It is reciprocal of time period

Amplitude (A):

The maximum displacement of a vibrating body on either side from its mean position is called its amplitude.

MOTION OF MASS ATTACHED TO SPRING HORIZONTALLY

One of the simplest types of oscillatory motion is that of mass-spring system . If the spring is stretched or compressed through a small displacement x from its mean position, it exerts a force F on the mass.

According to Hooke’s law this force is directly proportional to the change in length x of the spring i.e., $$ F=-kx \; \; \; \; \cdot \cdot \cdot \cdot (1)$$ where x is the displacement of the mass from its mean position O, and k is a constant called the spring constant defined as $$k = - \frac{F}{x} $$ The value of k is a measure of the stiffness of the spring. Stiff springs have large value of k and soft springs have small value of k. $$ As \;\; \; F = ma $$ $$ Therefore,\; eq\;(1)\;becomes \;\;\;\;ma=kx$$ $$ or \; \; a= - \frac{k}{m}x \; \; \; \cdot \cdot \cdot \cdot (2) $$ $$ a \propto -x $$ It means that the acceleration of a mass attached to a spring is directly proportional to its displacement from the mean position. Hence, the horizontal motion of a mass-spring system is an example of simple harmonic motion.

The negative sign in above means that the force exerted by the spring is always directed opposite to the displacement of the mass.
Because the spring force always acts towards the mean position, it is sometimes called a restoring force. A restoring force always pushes or pulls the object performing oscillatory motion towards the mean position.

Initially the mass m is at rest in mean position O and the resultant force on the mass is zero.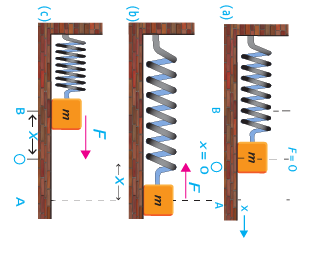 Suppose the mass is pulled through a distance x up to extreme position A and then released (Fig.10.1-b). The restoring force exerted by the spring on the mass will pull it towards the mean position O. Due to the restoring force the mass moves back, towards the mean position O. The magnitude of the restoring force decreases with the distance from the mean position and becomes zero at O.

However, the mass gains speed as it moves towards the mean position and its speed becomes maximum at O. Due to inertia the mass does not stop at the mean position O but continues its motion and reaches the extreme position B. As the mass moves from the mean position O to the extreme position B, the restoring force acting on it towards the mean position steadily increases in strength. Hence the speed of the mass decreases as it moves towards the extreme position B. The mass finally comes briefly to rest at the extreme position B. Ultimately the mass returns to the mean position due to the restoring force.

This process is repeated, and the mass continues to oscillate back and forth about the mean position O. Such motion of a mass attached to a spring on a horizontal frictionless surface is known as Simple Harmonic Motion (SHM).

Advanced Concepts:

Time Period:

Time required for one vibration of SHM is called Time Period. In one complete round trip body covers the angular displacement 2π radians with angular speed ω then time period is given by $$ T=\frac{2\pi}{\omega} \;\;\;\;\; (2)$$ But from Simple Harmonic motion of projection of body moving in circle with uniform circular speed we know that $$a=-\omega^2 x$$ But from equation (1) $$ a= -\frac{k}{m}x $$ $$ so \; \; \; -\frac{k}{m}x = -x\omega^2 $$ $$ \omega = \sqrt{\frac{k}{m}} $$ The time period T of the simple harmonic motion of a mass ‘m’ attached to a spring can be calculates by putting this value in eq (2) $$ T= 2 \pi \sqrt{\frac{m}{k}} $$

Frequency :

Instantaneous Displacement:

As we know from the motion of projection of a body moving in circle that instantaneous displacement is $$ x=x_{0} sin\omega t $$ putting value of ω $$x=x_{0}sin\sqrt{\frac{k}{m}}t $$

Instantaneous Velocity:

Instantaneous velocity v is given by $$ v=\omega \sqrt{x^2_{0} – x^2} $$ $$ v=\omega \sqrt{x^2_{0}(1- \frac{x^2}{x^2_{0}}) }$$ $$ v=\omega x_{0}\sqrt{(1- \frac{x^2}{x^2_{0}}) }$$ putting value of ω $$ v= x_{0}\sqrt{\frac{k}{m}}\sqrt{(1- \frac{x^2}{x^2_{0}})} \;\;\;\;\; \cdot \cdot\cdot\cdot (2)$$ We get maximum velocity v₀ when x=0 $$ so \; \; \; v_{0}=x_{0}\sqrt{ \frac{k}{m} } $$ $$ then \; eq(2)\;becomes \;\;\;\; v= v_{0} \sqrt{(1- \frac{x^2}{x^2_{0}})}$$

Energy Conservation in Mass_spring system:

Let us consider the case of vibrating mass-spring system. When the mass m is pulled slowly, the spring is stretched by an amount x₀ against the elastic restoring force F. It is assumed that stretching is done slowly so that acceleration is zero. According to Hook’s Law $$F=kx_{0}$$ $$ when\; displacement \;= 0 \;\;\;\; force = 0 $$ $$when \;displacement= x_{0} \;\;\;\; force=kx_{0}$$ $$Average \;Force \; F= \frac{0+kx_{0}}{2} = \frac{1}{2}kx_{0}$$ Work done in dispalcing the mass m through x₀ is $$W=Fd = \frac{1}{2}kx_{0} \times x_{0} $$ $$ \;\;\;\; = \frac{1}{2}kx^2_{0} $$ This work appears as elastic potential energy of the spring

Hence $$P.E= \frac{1}{2}kx^2_{0} $$ This equation gives maximum P.E. at the extreme positions. Thus $$ P.E_{max}=\frac{1}{2}kx^2_{0} $$ At any instance t , if the displacement is x, the P.E. at that instant is given by $$ P.E= \frac{1}{2}kx^2 $$

Instantaneous Velocity:

The velocity at that instant is given by equation 2 $$v= x_{0} \sqrt{[\frac{k}{m}](1-\frac{x^2}{x^2_{0}})} $$ $$ As \;\;\;\;K.E = \frac{1}{2}mv^2 $$ $$ so \;\;\;\; K.E = \frac{1}{2}m x^2_{0}[\frac{k}{m}] [1- \frac{x^2}{x^2_{0}}]$$ $$ K.E= \frac{1}{2}k(x^2_{0}-x^2) $$ The K.E is maximum when x=0 i.e when the mass is at mean positions $$ K.E_{max}= \frac{1}{2}kx^2_{0} $$ For any displacement the total energy is equal to the sum of P.E and K.E at that point.

Hence 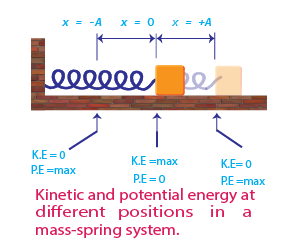$$ E_{total}=P.E + K.E $$ $$ \;\;\;\; = \frac{1}{2}kx^2 + \frac{1}{2}k(x^2_{0}-x^2) $$ $$ \;\;\;\; = \frac{1}{2}kx^2_{0} $$ Thus the total energy of vibrating mass and spring is constant. When $$ at \;\; x=0 \;\;\;\; K.E = maximum \;\;\;\; P.E = 0 $$ $$ at\;\; x=x_{0} \;\;\;\; K.E = 0 \;\;\;\; P.E= maximum $$